FDTD算法总结

news/发布时间2024/5/14 17:40:37

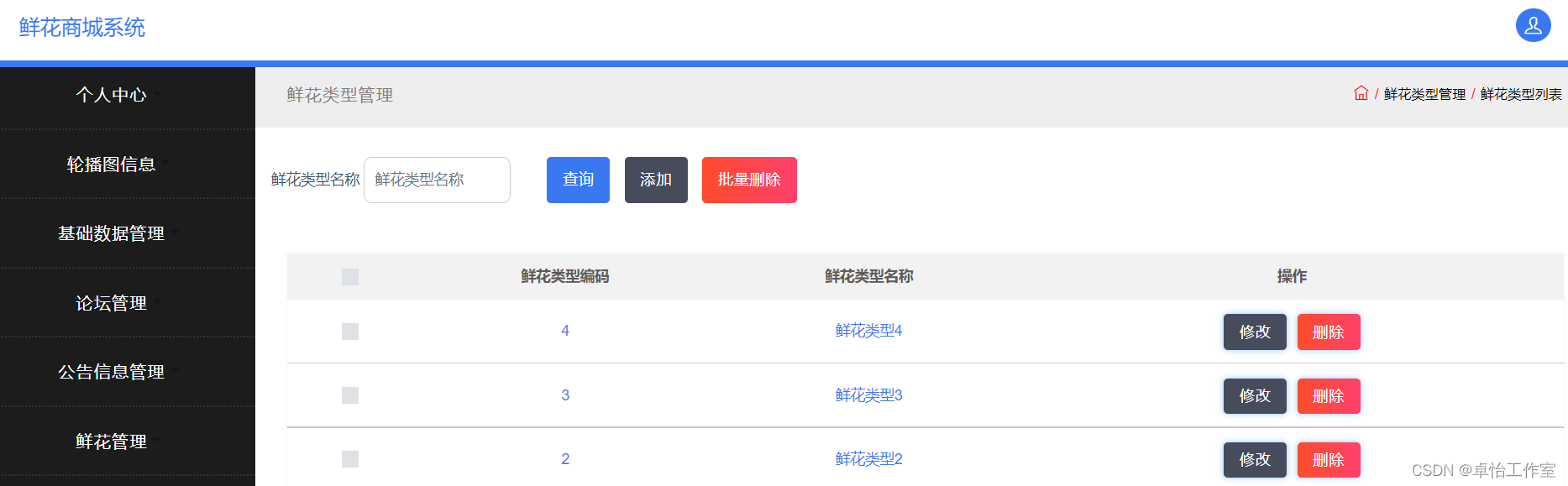
计算电磁学(Computational Electromagnetics, CEM)是通过数值计算来研究电磁场的交叉学科。

数值求解电磁学问题的方法可以分成频域(Frequency Doamin, FD)、时域(Time Domain, TD)等两类。

频域法基于时谐微分，通过对多个采样值的傅里叶逆变换得到所需的脉冲响应，使用这种方法，每次计算只能求得一个频率点上的响应。这类方法又可进一步分成低频算法、高频算法等两类。低频算法包括矩量法(Method of Moment, MoM)、频域有限差分(Finite Difference Frequency Doamin, FDFD)等；高频算法包括几何光学法、物理光学法等。

时域法按时间步进求得有关场量，一次求解可以获得很宽频带范围内的解。这类方法包括时域有限差分(Finite Difference Time Domain，FDTD)、时域有限单元(Finite Element Time Domain，FETD)等。

在时域法中，最为著名的就是FDTD。因此，本文拟对FDTD算法涉及的数理模型、数值模型等内容进行简要介绍。

注1：限于研究水平，分析难免不当，欢迎批评指正。

注2：文章内容会不定期更新。

一、物理方程

1864年，Maxwell在前人理论和实验的基础之上，建立了统一的电磁场理论，并用一组数学方程揭示了宏观电磁场的基本规律，这就是著名的Maxwell方程组。

Maxwell方程组有四个方程组成：描述电荷如何产生电场的高斯定律；论述磁单极子不存在的高斯磁定律；描述电流和时变电场怎样产生磁场的安培环路定律；描述时变磁场如何产生电场的法拉第感应定律。

$\left\{\begin{matrix} \nabla \cdot \mathbf{D}=\rho\\ \nabla\cdot \mathbf{B}=0\\ \nabla\times \mathbf{H}=\boldsymbol{j}+\frac{\partial \boldsymbol{D}}{\partial t}\\ \nabla\times \mathbf{E}=-\frac{\partial \boldsymbol{B}}{\partial t} \end{matrix}\right.$

对于各向同性线性介质，物性方程为，

$\left\{\begin{matrix} \boldsymbol{D}=\varepsilon\boldsymbol{E}\\ \boldsymbol{B}=\mu \boldsymbol{H}\\ \boldsymbol{j}=\sigma \boldsymbol{E} \end{matrix}\right.$

在上述公式中，各符号含义如下：

$\boldsymbol{D}$	电感强度
$\rho$	电荷密度
$\boldsymbol{B}$	磁感强度
$\boldsymbol{E}$	电场强度
$\boldsymbol{H}$	磁场强度
$\boldsymbol{j}$	传导电流密度
$\varepsilon$	介电常数	在真空中， $\varepsilon=\varepsilon_{0}=8.8542\times 10^{-12} C^2/N\cdot m^2$
$\mu$	磁导率	在真空中， $\mu =\mu_{0}=4\pi \times 10^{-7} N\cdot s^2/C^2$
$\sigma$	电导率

在三维笛卡尔坐标系下，有

$\frac{\partial E_{x}}{\partial x}+\frac{\partial E_{y}}{\partial y}+\frac{\partial E_{z}}{\partial z}=\frac{\rho }{\varepsilon }$

$\frac{\partial H_{x}}{\partial x}+\frac{\partial H_{y}}{\partial y}+\frac{\partial H_{z}}{\partial z}=0$

$\begin{matrix} \frac{\partial H_{y}}{\partial z}-\frac{\partial H_{z}}{\partial y}=\sigma E_{x}+\varepsilon \frac{\partial E_{x}}{\partial t}\\ \frac{\partial H_{z}}{\partial x}-\frac{\partial H_{x}}{\partial z}=\sigma E_{y}+\varepsilon \frac{\partial E_{y}}{\partial t}\\ \frac{\partial H_{y}}{\partial x}-\frac{\partial H_{x}}{\partial y}=\sigma E_{z}+\varepsilon \frac{\partial E_{z}}{\partial t} \end{matrix}$

$\begin{matrix} \frac{\partial E_{y}}{\partial z}-\frac{\partial E_{z}}{\partial y}=-\mu \frac{\partial H_{x}}{\partial t}\\ \frac{\partial E_{z}}{\partial x}-\frac{\partial E_{x}}{\partial z}=-\mu \frac{\partial H_{y}}{\partial t}\\ \frac{\partial E_{y}}{\partial x}-\frac{\partial E_{x}}{\partial y}=-\mu \frac{\partial H_{z}}{\partial t} \end{matrix}$

二、数值模型

FDTD是美籍华人K.S. Yee 于1966 年提出的求解微分形式Maxwell方程组的数值方法。FDTD在时域上直接求解微分形式的Maxwell方程组，

2.1 空间离散

在FDTD中，Yee使用Yee Cell在空间上交叉布置电场、磁场分量。电场分量放置到Yee单元各棱的中间，方向平行于各棱；磁场分量放置到Yee单元各面中心，方向平行于各面法线。

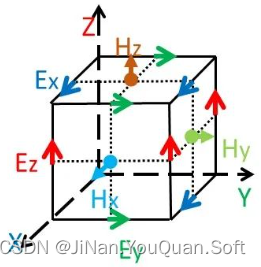
这样，每个电场分量由四个磁场分量环绕；每个磁场分量也由四个电场分量环绕。

对于麦克斯韦-安培定律与法拉第电磁感应定律，采用中心差分来离散磁场旋度与电场旋度。

为对于编号为 $\left ( i,j,k \right )$ 的Yee Cell，其中 $i\in \left [ 0, n_{x}\right )$ ， $j\in \left [ 0, n_{y}\right )$ ， $k\in \left [ 0, n_{z}\right )$ ， $n_{x}$ 、 $n_{y}$ 、 $n_{z}$ 为计算域在三个坐标轴方向的网格数，

可得法拉第感应定律、安培定律在空间域上的半离散格式，

$\begin{matrix}-\mu \frac{\partial H_{x}\left ( i,j,k \right )}{\partial t}= \frac{E_{y}\left ( i,j,k \right )-E_{y}\left ( i,j,k-1 \right )}{\Delta z}-\frac{E_{z}\left ( i,j,k \right )-E_{z}\left ( i,j-1,k \right )}{\Delta y}\\ -\mu \frac{\partial H_{y}\left ( i,j,k \right )}{\partial t}=\frac{E_{z}\left ( i,j,k \right )-E_{z}\left ( i-1,j,k \right )}{\Delta x}-\frac{E_{x}\left ( i,j,k \right )-E_{x}\left ( i,j,k-1 \right )}{\Delta z}\\ -\mu \frac{\partial H_{z}\left ( i,j,k \right )}{\partial t}=\frac{E_{y}\left ( i,j,k \right )-E_{y}\left ( i-1,j,k \right )}{\Delta x}-\frac{E_{x}\left ( i,j,k \right )-E_{x}\left ( i,j-1,k \right )}{\Delta y} \end{matrix}$

$\begin{matrix} \varepsilon \frac{\partial E_{x}\left ( i,j,k \right )}{\partial t}+\sigma E_{x}\left ( i,j,k \right )=\frac{H_{y}\left ( i,j,k \right )-H_{y}\left ( i,j,k-1 \right )}{\Delta z}-\frac{H_{z}\left ( i,j,k \right )-H_{z}\left ( i,j-1,k \right )}{\Delta y}\\ \varepsilon \frac{\partial E_{y}\left ( i,j,k \right )}{\partial t}+\sigma E_{y}\left ( i,j,k \right )=\frac{H_{z}\left ( i,j,k \right )-H_{z}\left ( i-1,j,k \right )}{\Delta x}-\frac{H_{x}\left ( i,j,k \right )-H_{x}\left ( i-1,j,k \right )}{\Delta z}\\ \varepsilon \frac{\partial E_{z}\left ( i,j,k \right )}{\partial t}+\sigma E_{z}\left ( i,j,k \right )= \frac{H_{y}\left ( i,j,k \right )-H_{y}\left ( i-1,j,k \right )}{\Delta x}-\frac{H_{x}\left ( i,j,k \right )-H_{x}\left ( i,j-1,k \right )}{\Delta y}\end{matrix}$

2.2 时间离散

在时间域上，FDTD采用蛙跳格式，由此可得法拉第感应定律、安培环路定律在时间域上的半离散格式，

$\begin{matrix} -\mu \frac{H_{x}^{n+\frac{1}{2}}-H_{x}^{n-\frac{1}{2}}}{\Delta t}=\frac{\partial E_{y}^{n}}{\partial z}-\frac{\partial E_{z}^{n}}{\partial y}\\ -\mu \frac{H_{y}^{n+\frac{1}{2}}-H_{y}^{n-\frac{1}{2}}}{\Delta t}=\frac{\partial E_{z}^{n}}{\partial x}-\frac{\partial E_{x}^{n}}{\partial z}\\ -\mu \frac{H_{z}^{n+\frac{1}{2}}-H_{z}^{n-\frac{1}{2}}}{\Delta t}=\frac{\partial E_{y}^{n}}{\partial x}-\frac{\partial E_{x}^{n}}{\partial y} \end{matrix}$

$\begin{matrix}\varepsilon \frac{E_{x}^{n+1}-E_{x}^{n}}{\Delta t}+ \sigma E_{x}^{n+\frac{1}{2}}=\frac{\partial H_{y}}{\partial z}-\frac{\partial H_{z}}{\partial y}\\ \varepsilon \frac{E_{y}^{n+1}-E_{y}^{n}}{\Delta t}+\sigma E_{y}^{n+\frac{1}{2}}=\frac{\partial H_{z}}{\partial x}-\frac{\partial H_{x}}{\partial z}\\ \varepsilon \frac{E_{z}^{n+1}-E_{z}^{n}}{\Delta t}+\sigma E_{z}^{n+\frac{1}{2}}=\frac{\partial H_{y}}{\partial x}-\frac{\partial H_{x}}{\partial y} \end{matrix}$

2.3 FDTD差分方程组

结合法拉第感应定律、安培环路定律在空间域、时间域上的离散格式，可得最终差法方程组，

$\begin{matrix}-\mu \frac{H_{x}^{n+\frac{1}{2}}\left ( i,j,k \right )-H_{x}^{n-\frac{1}{2}}\left ( i,j,k \right )}{\Delta t}= \frac{E_{y}^{n}\left ( i,j,k \right )-E_{y}^{n}\left ( i,j,k-1 \right )}{\Delta z}-\frac{E_{z}^{n}\left ( i,j,k \right )-E_{z}^{n}\left ( i,j-1,k \right )}{\Delta y}\\ -\mu \frac{H_{y}^{n+\frac{1}{2}}\left ( i,j,k \right )-H_{y}^{n-\frac{1}{2}}\left ( i,j,k \right )}{\Delta t}=\frac{E_{z}^{n}\left ( i,j,k \right )-E_{z}^{n}\left ( i-1,j,k \right )}{\Delta x}-\frac{E_{x}^{n}\left ( i,j,k \right )-E_{x}^{n}\left ( i,j,k-1 \right )}{\Delta z}\\ -\mu \frac{H_{z}^{n+\frac{1}{2}}\left ( i,j,k \right )-H_{z}^{n-\frac{1}{2}}\left ( i,j,k \right )}{\Delta t}=\frac{E_{y}^{n}\left ( i,j,k \right )-E_{y}^{n}\left ( i-1,j,k \right )}{\Delta x}-\frac{E_{x}^{n}\left ( i,j,k \right )-E_{x}^{n}\left ( i,j-1,k \right )}{\Delta y} \end{matrix}$

$\begin{matrix} \varepsilon \frac{E_{x}^{n+1}\left ( i,j,k \right )-E_{x}^{n+1}\left ( i,j,k \right )}{\Delta t}+\sigma E_{x}^{n+\frac{1}{2}}\left ( i,j,k \right )=\frac{H_{y}^{n+\frac{1}{2}}\left ( i,j,k \right )-H_{y}^{n+\frac{1}{2}}\left ( i,j,k-1 \right )}{\Delta z}-\frac{H_{z}^{n+\frac{1}{2}}\left ( i,j,k \right )-H_{z}^{n+\frac{1}{2}}\left ( i,j-1,k \right )}{\Delta y}\\ \varepsilon \frac{E_{y}^{n+1}\left ( i,j,k \right )-E_{y}^{n}\left ( i,j,k \right )}{ \Delta t}+\sigma E_{y}^{n+\frac{1}{2}}\left ( i,j,k \right )=\frac{H_{z}^{n+\frac{1}{2}}\left ( i,j,k \right )-H_{z}^{n+\frac{1}{2}}\left ( i-1,j,k \right )}{\Delta x}-\frac{H_{x}^{n+\frac{1}{2}}\left ( i,j,k \right )-H_{x}^{n+\frac{1}{2}}\left ( i-1,j,k \right )}{\Delta z}\\ \varepsilon \frac{E_{z}^{n+1}\left ( i,j,k \right )-E_{z}^{n}\left ( i,j,k \right )}{\Delta t}+\sigma E_{z}^{n+\frac{1}{2}}\left ( i,j,k \right )= \frac{H_{y}^{n+\frac{1}{2}}\left ( i,j,k \right )-H_{y}^{n+\frac{1}{2}}\left ( i-1,j,k \right )}{\Delta x}-\frac{H_{x}^{n+\frac{1}{2}}\left ( i,j,k \right )-H_{x}^{n+\frac{1}{2}}\left ( i,j-1,k \right )}{\Delta y}\end{matrix}$

2.4 边界条件

由于数值模拟只能选取有限区域作为计算域进行仿真计算，因此，在计算域边界处，需要给出吸收边界条件。

目前效果最好的吸收边界层是Berenger于1994年提出的完美匹配层(Perfect Matched Layer, PML)。完全匹配层是数学上在FDTD区域截断边界处虚拟设置一种特殊介质层,通过合理地选择PML的本构参数,能够使FDTD计算域的外行电磁波无反射地穿过分界面,并在吸收层内被迅速吸收分解。

2.5 源项处理

根据源项随时间的变化，源项可分为周期性源项和非周期性源项。

根据源项几何形状，可分为点源、线源、面源等。

2.6 收敛性、稳定性条件

设 $c$ 为计算空间内电磁波最大传播速度， $\Delta t$ 为时间步2长， $\delta$ 为网格尺寸，则有

对于三维均匀网格，时间步长 $\Delta t$ 、网格尺寸 $\delta$ 需要满足Courant条件： $c\Delta t\leq \frac{\delta }{\sqrt{3}}$ 。

对于二维均匀网格，时间步长 $\Delta t$ 、网格尺寸 $\delta$ 需要满足Courant条件： $c\Delta t\leq \frac{\delta }{\sqrt{2}}$ 。

对于二维均匀网格，时间步长 $\Delta t$ 、网格尺寸 $\delta$ 需要满足Courant条件： $c\Delta t\leq \delta$ 。

三、实现与测试

参考文献

K S Yee .Numerical solution of initial boundary value problems involving maxwell's equations in isotropic media[J].IEEE Transactions on Antennas & Propagation, 1966, 14(5):302-307.DOI:10.1109/TAP.1966.1138693.
赖生建. 计算电磁学讲义.
梁铨廷. 物理光学(第五版). 2018